5. Vectors
c. Scalar Multiplication
2. Geometric Construction
How are the magnitude and direction of \(c\,\vec v\) related to those of \(\vec v\)? Knowing this will allow us to give a geometric description of scalar multiplication:
First the magnitude: \[\begin{aligned} |c\,\vec v| &=\sqrt{\left(c\,v_1\right)^2+\left(c\,v_2\right)^2} =\sqrt{c^2\left({v_1}^2+{v_2}^2\right)} \\ &=\sqrt{c^2}\sqrt{ {v_1}^2+{v_2}^2} =|c|\,|\vec v| \end{aligned}\] Notice that \(\sqrt{c^2}=|c|\) not \(c\), in case \(c\) is negative. Thus, the vector \(c\,\vec v\) is \(|c|\) times as long as \(\vec v\).
Next the direction. Recall that the direction is its unit vector. So let \(\vec w=c\,\vec v=\left\langle c\,v_1,c\,v_2\right\rangle\). Then \(|\vec w|=|c|\,|\vec v|\). So \[\begin{aligned} \hat w &=\dfrac{\vec w}{|\vec w|} =\left\langle\dfrac{c\,v_1}{|c|\,|\vec v|}, \dfrac{c\,v_2}{|c|\,|\vec v|}\right\rangle \\ &=\dfrac{c}{|c|} \left\langle\dfrac{v_1}{|\vec v|}, \dfrac{v_2}{|\vec v|}\right\rangle =\dfrac{c}{|c|}\hat v \end{aligned}\] Consequently:
- If \(c \gt 0\), so that \(|c|=c\), then \(\hat w=\hat v\). So \(\vec w=c\,\vec v\) has the same direction as \(\vec v\).
- If \(c \lt 0\), so that \(|c|=-c\), then \(\hat w=-\hat v\). So \(\vec w=c\,\vec v\) points opposite to the direction of \(\vec v\).
- If \(c=0\), then \(0\,\vec v=\left\langle0,0\right\rangle=\vec 0\). This is the zero vector which has \(0\) length and does not point anywhere.
We summarize:
Geometric Construction
Given a scalar (real number) \(c\) and a vector
\(\vec v=\left\langle v_1,v_2\right\rangle\),
then the scalar product \(c\,\vec v\) satisfies:
If \(c \gt 0\), then \(|c\,\vec v|=c\,|\vec v|\) and \(c\,\vec v\)
points in the same direction as \(\vec v\).
If \(c < 0\), then \(|c\,\vec v|=-c\,|\vec v|\) and \(c\,\vec v\)
points in the opposite direction to \(\vec v\).
If \(c=0\), then \(c\,\vec v=\vec 0\).
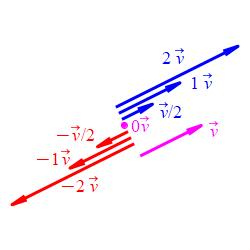
Further, if \(|c| \gt 1\) then \(c\,\vec v\) stretches \(\vec v\)
and if \(|c| \lt 1\) then \(c\,\vec v\) shrinks \(\vec v\).
This is shown in the diagram for
\(c=2,1,\dfrac{1}{2},0,-\dfrac{1}{2},-1,-2\).
If \(\vec a=\left\langle3,-2\right\rangle\), describe in words the vectors \(3\,\vec a=\left\langle9,-6\right\rangle\) and \(-\dfrac{1}{3}\,\vec a =\left\langle-1,\dfrac{2}{3}\right\rangle\).
\(3\,\vec a\) is the vector in the same direction as \(\vec a\)
but \(3\) times as long.
\(-\dfrac{1}{3}\,\vec a\) is the vector in the opposite direction from
\(\vec a\) but \(\dfrac{1}{3}\) as long.
Consider the vector \(\vec a\) shown at the right. Which of the following is \(-\,\dfrac{1}{3}\vec a\)?





\(\dfrac{1}{3}\times\vec a=\)
 \(-\,\dfrac{1}{3}\times\vec a=\)
\(-\,\dfrac{1}{3}\times\vec a=\)

This is bullet (A).
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum